8 min to read
기본 정렬 알고리즘
기본 정렬 알고리즘에 대해 알아봅니다.
정렬 알고리즘에 대하여 공부한 내용을 정리합니다.
정렬은 한 자료 구조 안에 있는 데이터를 비교하는 기준으로 순서대로 나타내는 것입니다.
정렬의 시간 복잡도는 O(N^2), O(N log N), O(N + ?) 등으로 나뉩니다.
이번 장에서는 시간 복잡도가 O(N^2) 에 해당 되는 정렬 알고리즘에 대해 포스팅 하겠습니다.
Selection Sort
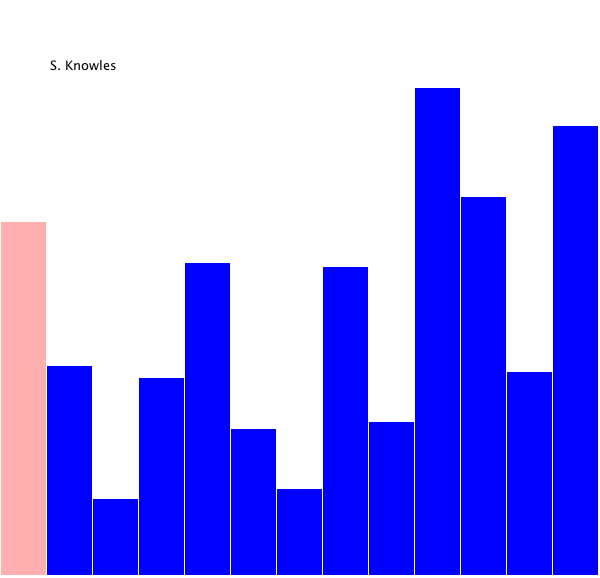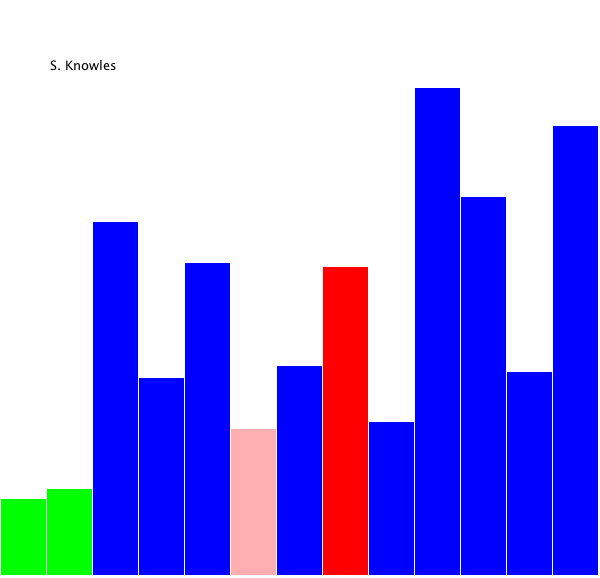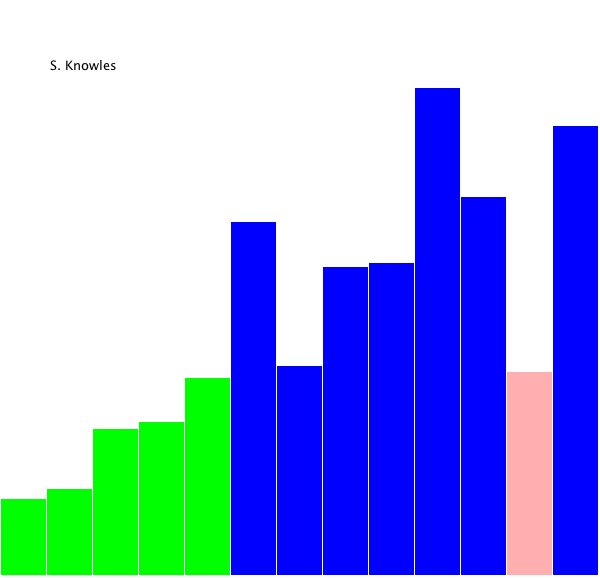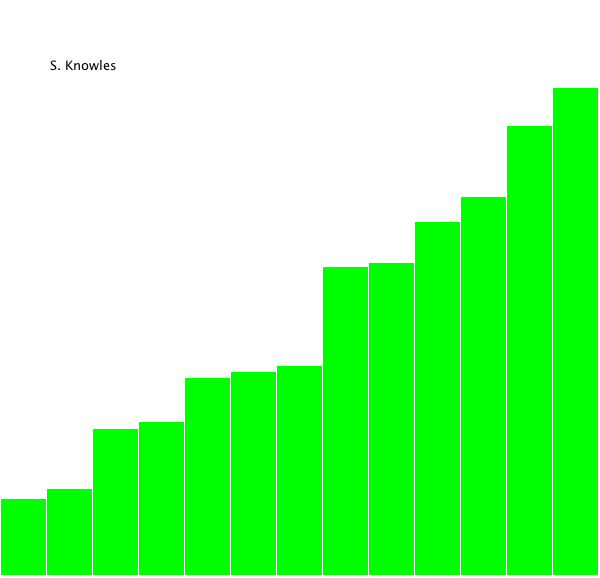
- 최댓값(내림차순) 혹은 최솟값(오름차순) 에 해당 된 인덱스를 찾아 현 자리와 교체하는 방식.
- 시간 복잡도는 O(n^2), 공간 복잡도는 O(1).
swap함수가 필요한 정렬 알고리즘.
소스 코드는 아래와 같습니다.
import java.util.Arrays;
public class SelectionSort {
static void swap(int[] arr, int a, int b){
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
// 최솟값 인덱스 찾는 함수
static int min_index(int start, int[] arr){
int min = Integer.MAX_VALUE;
int idx = start;
for(int k = start; k < arr.length; k++){
if(min > arr[k]){
min = Math.min(min, arr[k]);
idx = k;
}
}
return idx;
}
static void selection_sort(int[] arr){
for(int k = 0; k < arr.length - 1; k++){
int idx = min_index(k, arr);
swap(arr, k, idx);
}
}
public static void main(String[] args){
int[] array = new int[] { 9, 2, 5, 3, 6, 1, 7, 8, 10, 4 };
selection_sort(array);
System.out.println(Arrays.toString(array)); // 결과 값 출력
}
}
Bubble Sort
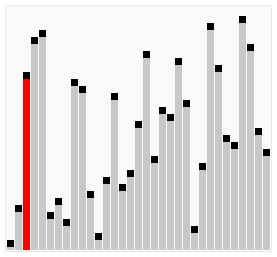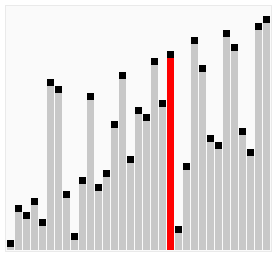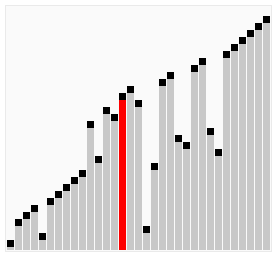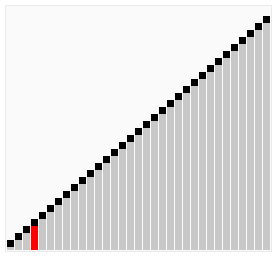
- 연속된 두 인덱스를 비교하여, 우측의 값이 작으면 현 자리와 교체하는 방식.
- 원소의 이동이 거품 처럼 수면에 올라가는 것과 유사하여 지어진 별칭.
- 시간 복잡도는 O(n^2), 공간 복잡도는 O(1).
swap함수가 필요한 정렬 알고리즘.
소스 코드는 아래와 같습니다.
import java.util.Arrays;
public class BubbleSort {
static void swap(int[] arr, int a, int b){
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
static void bubble_sort(int[] arr){
for(int k = arr.length - 1; k >= 1; k--){
boolean completed = true;
for(int l = 0; l < k; l++){
if(arr[l] > arr[l + 1]) {
swap(arr, l, l + 1);
completed = false;
}
}
if(completed) break;
}
}
public static void main(String[] args){
int[] array = new int[] { 9, 2, 5, 3, 6, 1, 7, 8, 10, 4 };
bubble_sort(array);
System.out.println(Arrays.toString(array));
}
}
Cocktail Shaker Sort
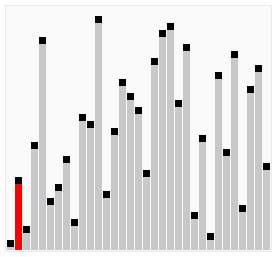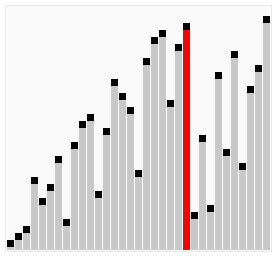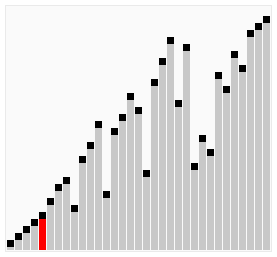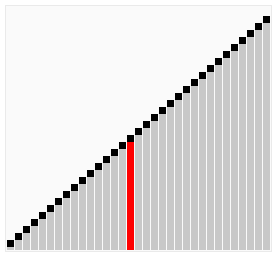
- 버블 정렬 중 교체가 안 일어나는 루프를 최소화 하기 위한 정렬 알고리즘.
- 오른쪽, 왼쪽, 오른쪽, 왼쪽… 진자의 움직임 처럼 정렬되는 알고리즘.
swapped변수로 정렬 진행 여부를 체크하여 반복문 루프를 최소화.
(물론, 버블 정렬에서도 가능한 일.)- 시간 복잡도는 O(n^2), 공간 복잡도는 O(1).
swap함수가 필요한 정렬 알고리즘.
소스 코드는 아래와 같습니다.
import java.util.Arrays;
public class CocktailShakerSort {
static void swap(int[] arr, int a, int b){
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
static void cocktail_shaker_sort(int[] arr){
boolean swapped = true;
int start = 0;
int end = arr.length;
while(swapped){
swapped = false;
for(int k = start; k < end - 1; k++){
if(arr[k] > arr[k + 1]) {
swap(arr, k, k + 1);
swapped = true;
}
}
if(!swapped) break;
end = end - 1;
for(int k = end - 1; k >= start; k--){
if(arr[k] > arr[k + 1]) {
swap(arr, k, k + 1);
swapped = true;
}
}
start = start + 1;
}
}
public static void main(String[] args){
int[] array = new int[] { 9, 2, 5, 3, 6, 1, 7, 8, 10, 4 };
cocktail_shaker_sort(array);
System.out.println(Arrays.toString(array));
}
}
Insertion Sort
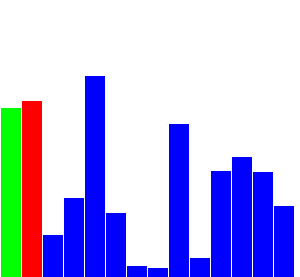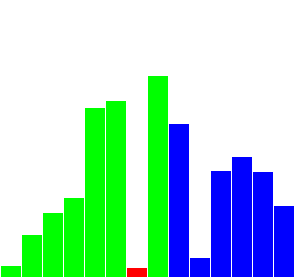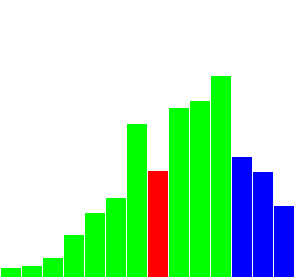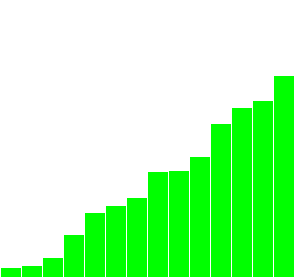
- 한 쪽 부분(오름차순이면 왼쪽)을 기준점으로 잡고 데이터를 점차 추가하는 방식.
- 정렬된 상태를 유지하기 때문에 안정적인 정렬(Stable Sort) 에 속함.
- 시간 복잡도는 O(n^2), 공간 복잡도는 O(1).
소스 코드는 아래와 같습니다.
import java.util.Arrays;
public class InsertionSort {
static void insert_sort(int[] arr){
for(int k = 1; k < arr.length; k++){
int value = arr[k];
int l;
for(l = k - 1; l >= 0 && arr[l] > value; l--)
arr[l + 1] = arr[l];
arr[l + 1] = value;
}
}
public static void main(String[] args){
int[] array = new int[] { 9, 2, 5, 3, 6, 1, 7, 8, 10, 4 };
insert_sort(array);
System.out.println(Arrays.toString(array));
}
}
안정 정렬(Stable Sort)
안정 정렬은 레코드의 Key 를 유지한 상태로, 값들의 순서를 유지하는 것입니다.
(정렬 알고리즘 방식이 아닌, 특성을 뜻하는 것입니다.)
대표적으로 삽입 정렬(Insertion Sort), 칵테일 쉐이커 정렬(Cocktail Shaker Sort), 버블 정렬(Bubble Sort), 병합 정렬(Merge Sort) 등이 있습니다.

Comments