13 min to read

보통 정렬 알고리즘

기본 정렬보다 조금 나은 보통 정렬 알고리즘에 대해 알아봅니다.

기본 정렬 알고리즘은 시간 복잡도가 O(N^2) 이기 때문에 실무에서는 잘 사용하지 않습니다.

그래서 구현하는 방법이 조금 어려울지 언정, 실무에서 많이 쓰이는 보통 정렬 알고리즘에 대해 알아 보겠습니다.

이번 장에서는 시간 복잡도가 O(N log N) 에 해당 되는 정렬 알고리즘에 대해 포스팅 하겠습니다.

Merge Sort

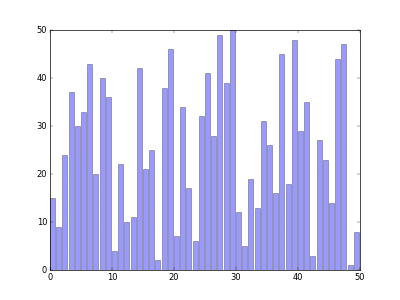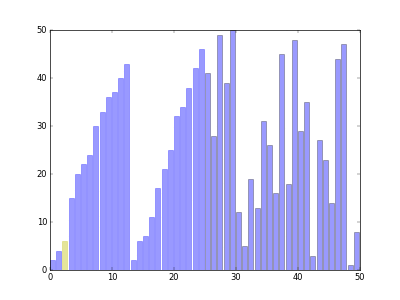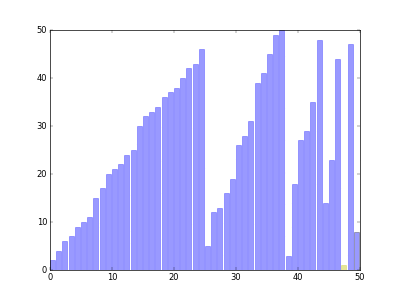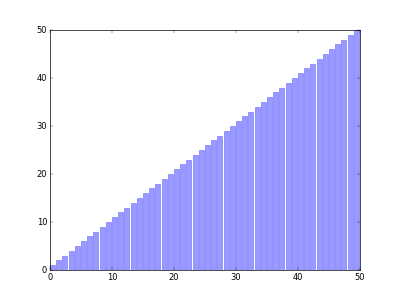
Merge_Sort_Anim

소스 코드는 아래와 같습니다.

import java.util.Arrays;

public class MergeSort {
    static void merge(int[] arr, int start, int mid, int end){
        int len = end - start + 1;
        int[] tmp = new int[len];

        int i = 0;
        int idx1 = start;
        int idx2 = mid + 1;

        // 일단 두 배열에 있는 값을 비교하여 작은 것을 넣어줍니다.
        while(idx1 <= mid && idx2 <= end){
            if(arr[idx1] < arr[idx2])
                tmp[i++] = arr[idx1++];
            else
                tmp[i++] = arr[idx2++];
        }

        // 나머지 처리(시작 - 중앙 부분)
        while(idx1 <= mid)
            tmp[i++] = arr[idx1++];

        // 나머지 처리(중앙 - 끝 부분)
        while(idx2 <= end)
            tmp[i++] = arr[idx2++];

        // 배열 복사
        for(int k = 0; k < len; k++)
            arr[start + k] = tmp[k];
    }

    static void merge_sort(int[] arr, int start, int end){
        if(start >= end) return;
        int mid = (start + end) / 2;
        merge_sort(arr, start, mid);
        merge_sort(arr, mid + 1, end);
        merge(arr, start, mid, end);
    }

    public static void main(String[] args){
        int[] array = new int[] { 9, 2, 5, 3, 6, 1, 7, 8, 10, 4 };
        merge_sort(array, 0, array.length - 1);
        System.out.println(Arrays.toString(array));
    }
}

Heap Sort

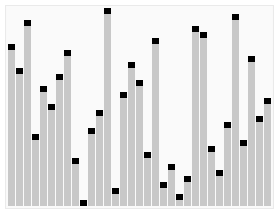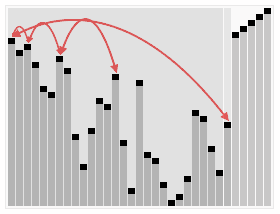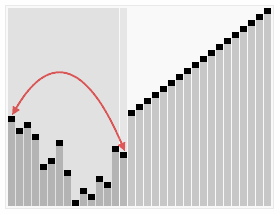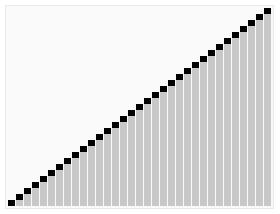
Heap_Sort_Anim

소스 코드는 아래와 같습니다.


import java.util.Arrays;

public class HeapSort {
    static void swap(int[] arr, int x, int y){
        int tmp = arr[x];
        arr[x] = arr[y];
        arr[y] = tmp;
    }

    // build_heap 메소드는 중앙 인덱스부터 0 까지 Heap 자료구조로
    static void build_heap(int[] arr){
        int end = arr.length - 1;
        for(int k = (end - 1) / 2; k >= 0; k--)
            heapify(arr, k, end);
    }

    // heapify 메소드는 배열을 Heap 자료구조로 정리하기 위한 용도입니다.
    static void heapify(int[] arr, int k, int end){
        int left = 2 * k + 1, right = 2 * k + 2;
        int smaller;
        if(right <= end)
            smaller = (arr[left] > arr[right]) ? left : right;
        else if(left <= end) smaller = left;
        else return;
        if(arr[smaller] > arr[k]){
            swap(arr, smaller, k);
            heapify(arr, smaller, end);
        }
    }

    static void heap_sort(int[] arr){
        build_heap(arr);
        for(int end = arr.length - 1; end >= 1; end--) {
            swap(arr, 0, end);
            heapify(arr, 0, end - 1);
        }
    }

    public static void main(String[] args){
        int[] array = new int[] { 9, 2, 5, 3, 6, 1, 7, 8, 10, 4 };
        heap_sort(array);
        System.out.println(Arrays.toString(array));
    }
}

Quick Sort

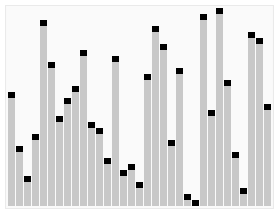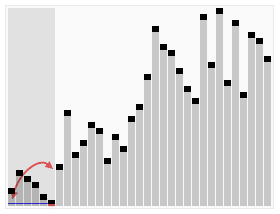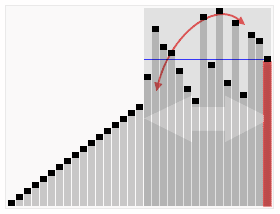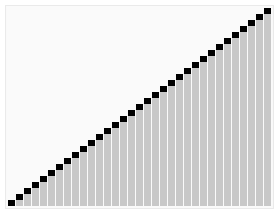
Quick_Sort_Anim

소스 코드는 아래와 같습니다.

import java.util.Arrays;

public class QuickSort {
    static void swap(int[] arr, int a, int b){
        int tmp = arr[a];
        arr[a] = arr[b];
        arr[b] = tmp;
    }

    static int partition(int[] arr, int from, int to){
        int value = arr[to]; // 기준 값은 끝탱이를 잡아도 큰 상관은 없습니다.
        int k = from - 1;
        for(int l = from; l <= to - 1; l++)
            if(arr[l] < value)
                swap(arr, ++k, l);
        swap(arr, k + 1, to); // 마지막에 끝탱이를 맨 가운데로 가져옵니다.
        return k + 1;
    }

    static void quick_sort(int[] arr, int start, int end){
        if(start >= end) return;
        int pivot = partition(arr, start, end);
        quick_sort(arr, start, pivot - 1);
        quick_sort(arr, pivot + 1, end);
    }

    public static void main(String[] args){
        int[] array = new int[] { 9, 2, 5, 3, 6, 1, 7, 8, 10, 4 };
        quick_sort(array, 0, array.length - 1);
        System.out.println(Arrays.toString(array));
    }
}

3-Way Partition Quick Sort

소스 코드는 아래와 같습니다.

import java.util.Arrays;

public class DualPivotQuickSort {
    static class Pair {
        int primary;
        int secondary;
        public Pair(int primary, int secondary){
            this.primary = primary;
            this.secondary = secondary;
        }
    }

    static void swap(int[] a, int x, int y){
        int tmp = a[x];
        a[x] = a[y];
        a[y] = tmp;
    }

    static Pair partition(int[] a, int start, int end){
        if(a[end - 1] > a[end]) swap(a, end - 1, end);

        int v1 = a[end - 1];
        int v2 = a[end];

        int i1 = start - 1;
        int i2 = start - 1;

        for(int k = start; k <= end - 2; k++){
            if(a[k] < v1) {
                swap(a, ++i1, k);
                if(i2 < i1) i2 = i1;
                else swap(a, ++i2, k);
            } else if(a[k] < v2) {
                swap(a, ++i2, k);
            } else continue;
        }

        swap(a, ++i1, end - 1);
        if(i2 < i1) i2 = i1;
        else swap(a, ++i2, end - 1);
        swap(a, ++i2, end);

        return new Pair(i1, i2);
    }

    static void three_way_quick_sort(int[] a, int start, int end){
        if(start >= end) return;
        Pair pivot = partition(a, start, end);
        three_way_quick_sort(a, start, pivot.primary - 1);
        three_way_quick_sort(a, pivot.primary + 1, pivot.secondary - 1);
        three_way_quick_sort(a, pivot.secondary + 1, end);
    }

    public static void main(String[] args){
        int[] array = new int[] { 9, 2, 5, 3, 6, 1, 7, 8, 10, 4, -2, -9, -3, -1, -7, -8, 0, 6 };
        three_way_quick_sort(array, 0, array.length - 1);
        System.out.println(Arrays.toString(array));
    }
}

Reference

정렬 과정을 비교하는 사이트 입니다.

이 사이트를 사용하면 더욱 시각화 된 정렬 과정을 보실 수 있습니다.

https://www.toptal.com/developers/sorting-algorithms